En este proyecto probamos y analizamos la efectividad de varios métodos para resolver sistemas de ecuaciones lineales. Estos sistemas están presentes en muchos aspectos del día a día, desde los modelos de lenguaje hasta la gestión de la cadena de suministro. Por lo tanto, es importante conocer cuáles son los métodos que ofrecen los resultados más precisos y eficientes. El objetivo de este proyecto era determinar qué métodos de resolución eran los más adecuados para las aplicaciones prácticas.
Resumen del proyecto
Resumen del proyecto
¿Puedes contarnos brevemente en qué consiste el proyecto que has estado desarrollando?
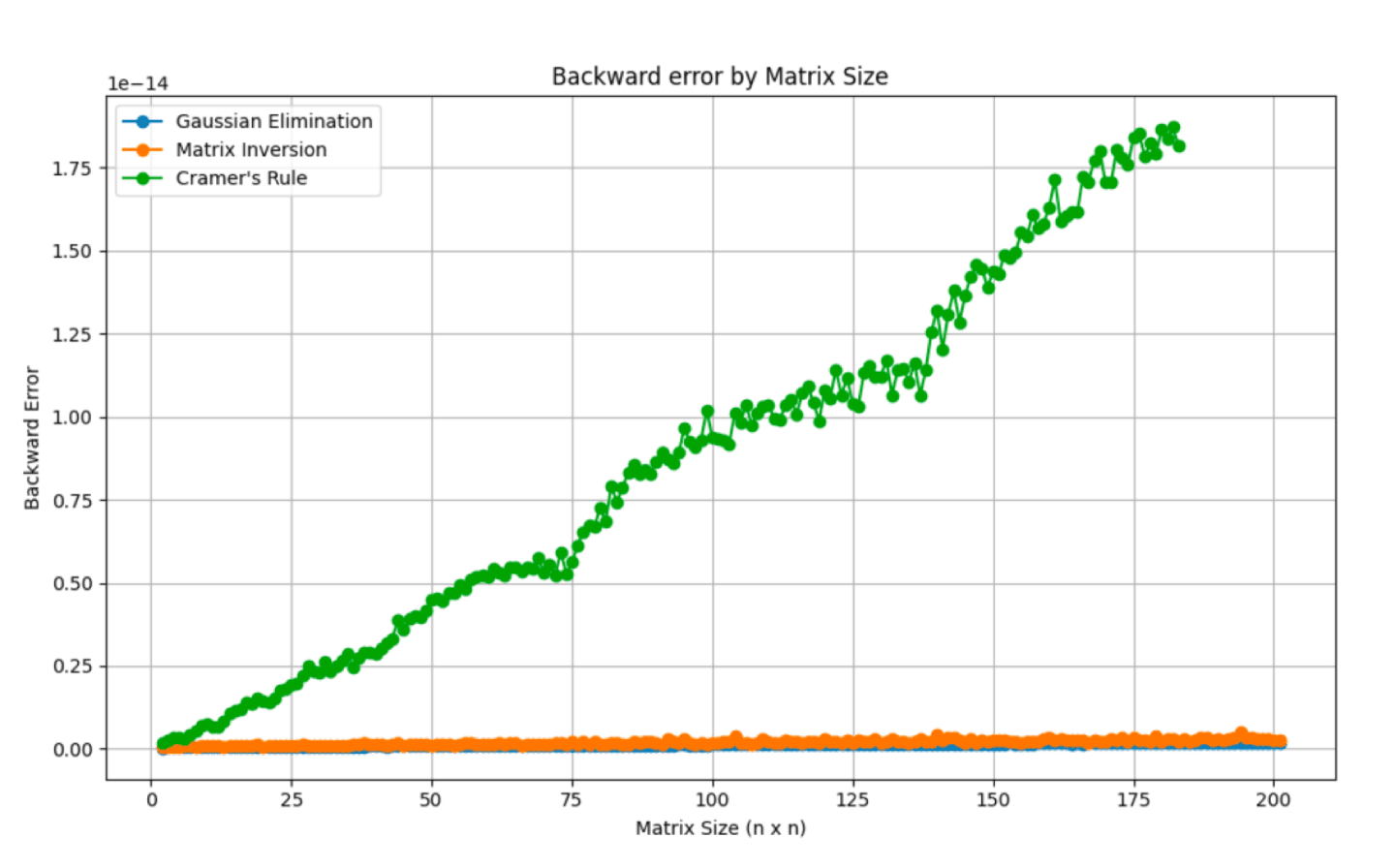
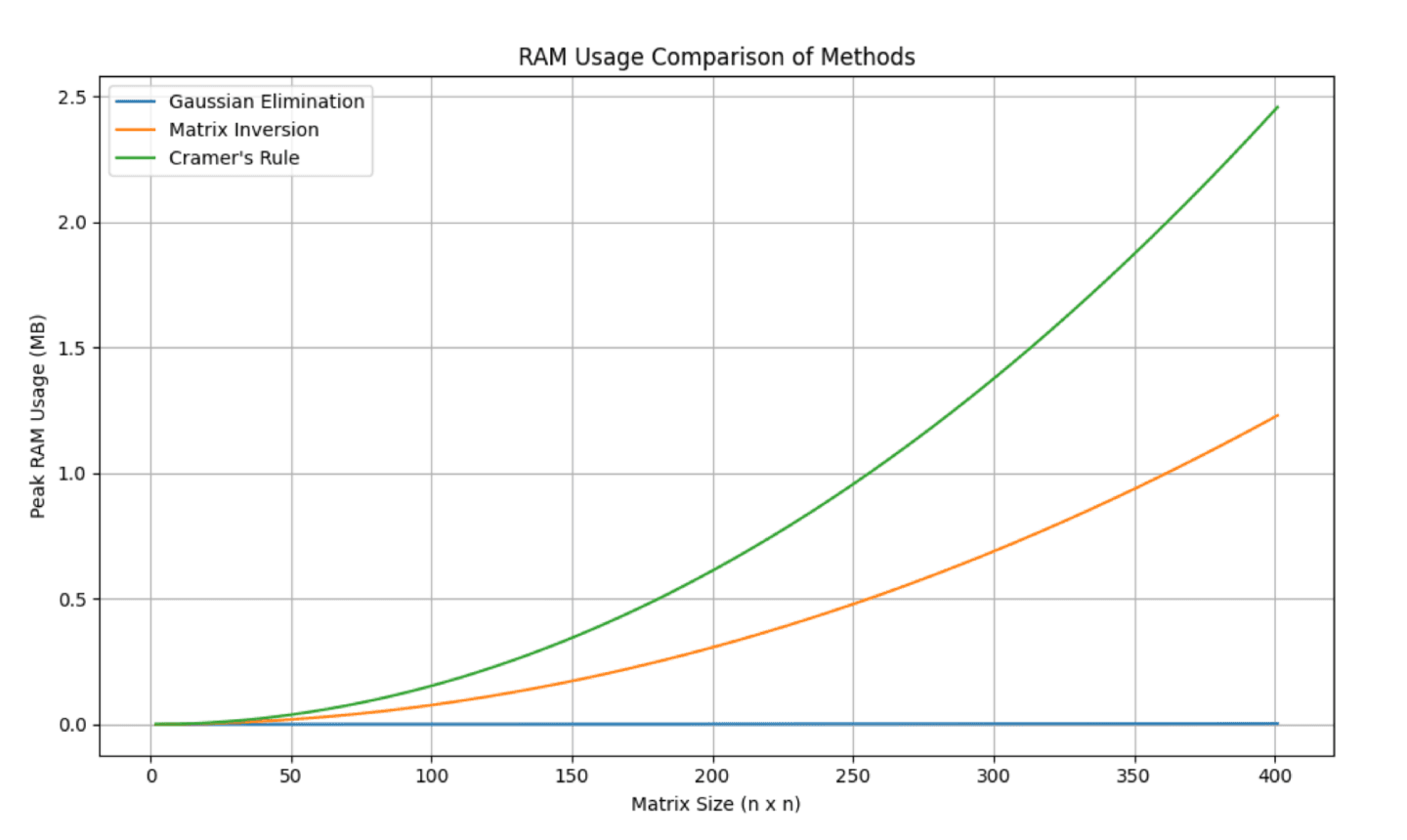
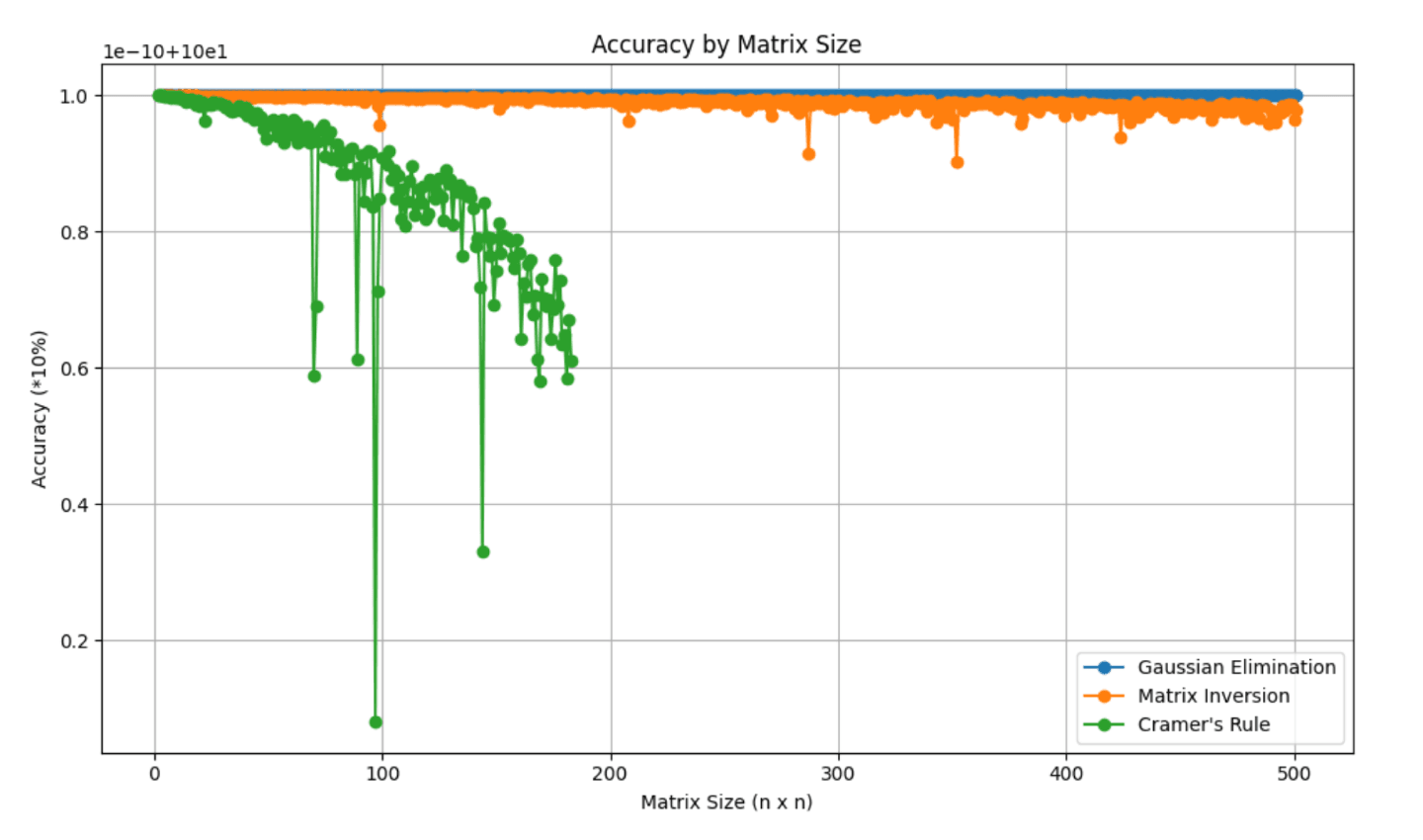
El objetivo principal de este proyecto es determinar cuáles son los métodos más eficientes para resolver sistemas de ecuaciones lineales. Dado que la mayoría de las aplicaciones reales de estos sistemas se encuentran en el campo de la tecnología, nuestras métricas de eficiencia fueron el uso de la RAM, el uso de la CPU, el error regresivo, la precisión y el tiempo de cálculo. Para implementar estas pruebas, generamos matrices aleatorias con tamaños que iban desde 2 x 2 hasta 200 x 200, y evaluamos cada método en función de estas métricas de rendimiento. Los métodos que decidimos probar fueron la regla de Cramer, la eliminación gaussiana y la inversión de matrices, tres técnicas que habitualmente se usan para resolver sistemas lineales. Cada uno de estos métodos se analizó en términos de complejidad computacional, estabilidad numérica y practicidad a medida que aumentaba el tamaño de la matriz. A continuación, los resultados se plasmaron en gráficos para analizar visualmente la eficiencia de cada método en matrices de diferente tamaño. Esta visualización nos ayudó a identificar la capacidad para escalar de cada método cuando aumenta el tamaño del problema, y también nos permitió analizar cómo los cambios en los parámetros afectan a los resultados.
Detalles técnicos
Detalles técnicos
¿Puedes explicar los aspectos técnicos del proyecto? ¿Qué software o qué herramientas utilizas?
El objetivo de nuestro proyecto era comparar tres enfoques clásicos para resolver ecuaciones lineales: la eliminación gaussiana, la inversión de matrices y la regla de Cramer. Implementamos estos métodos en Python, aprovechando sus bibliotecas. Concretamente, usamos NumPy para las operaciones matriciales, Matplotlib para la visualización, time para la medición del tiempo de ejecución, y psutil para monitorizar el uso de la RAM.
Para evaluar sistemáticamente el rendimiento de cada método, primero desarrollamos un generador de matrices aleatorias que creó matrices cuadradas y las soluciones vectoriales correspondientes con parámetros personalizables. Esto nos permitió probar los métodos bajo diferentes condiciones para analizar su eficacia. En el caso de la eliminación gaussiana, usamos la función integrada de NumPy para garantizar un rendimiento óptimo. Del mismo modo, para la inversión de matrices, utilizamos las funciones de NumPy para, primero, obtener la matriz inversa de la matriz de coeficientes y, a continuación, multiplicarla por la solución vectorial. Por último, para la regla de Cramer, optamos por la función determinante de NumPy para calcular repetidamente los determinantes de cada variable del sistema.
Para evaluar la efectividad de estos métodos, realizamos pruebas exhaustivas centradas en la precisión, la estabilidad numérica, el tiempo de ejecución y el uso de los recursos. Usamos la eliminación gaussiana de NumPy como punto de referencia para comparar la precisión de cada enfoque. El tiempo de ejecución se midió con la biblioteca de tiempos de Python, y usamos psutil para monitorizar la eficiencia computacional. Estas herramientas nos permitieron obtener datos sobre los puntos fuertes y las limitaciones de cada método.
Desafíos y soluciones
Desafíos y soluciones
¿Te enfrentaste a algún desafío importante durante el proyecto? ¿Cómo lo superaste? ¿Hay algún momento que destaques especialmente en cuanto a resolución de problemas?
Hubo un momento complicado en el que no podíamos completar una prueba de rendimiento. Intentamos trabajar en ella simultáneamente, pero nos dimos cuenta de que estábamos empeorando la situación. Entonces, reorganizamos las tareas y rotamos de una a otra. Esto permitió que todos pudiéramos ver las diferentes partes del proyecto, ya fuera haciendo comprobaciones o reformateando, para después volver al problema con una nueva perspectiva. Al final, pusimos las ideas en común y las implementamos de manera adecuada y efectiva.
Colaboración y trabajo en equipo
Colaboración y trabajo en equipo
¿Habéis colaborado con otros estudiantes o miembros del equipo en este proyecto? ¿Cómo contribuyó el trabajo en equipo al éxito o progreso del proyecto?
Éramos cuatro personas en el equipo, lo que nos permitió dividir las tareas de manera uniforme y eficiente. Sin embargo, fue importante volver atrás para asegurarnos de que todos los elementos estaban correctamente relacionados. Era fundamental que los scripts estuviesen alineados para obtener parámetros de entrada globales que después utilizaríamos cada uno de nosotros. Además, como hemos mencionado, una nueva perspectiva puede ser de gran ayuda en cualquier proyecto. Delegar el trabajo de acuerdo con las fortalezas y las preferencias de cada uno también fue un factor que nos benefició.
Aprendizajes y conclusiones
Aprendizajes y conclusiones
¿Qué lecciones has aprendido o qué habilidades has desarrollado trabajando en este proyecto?
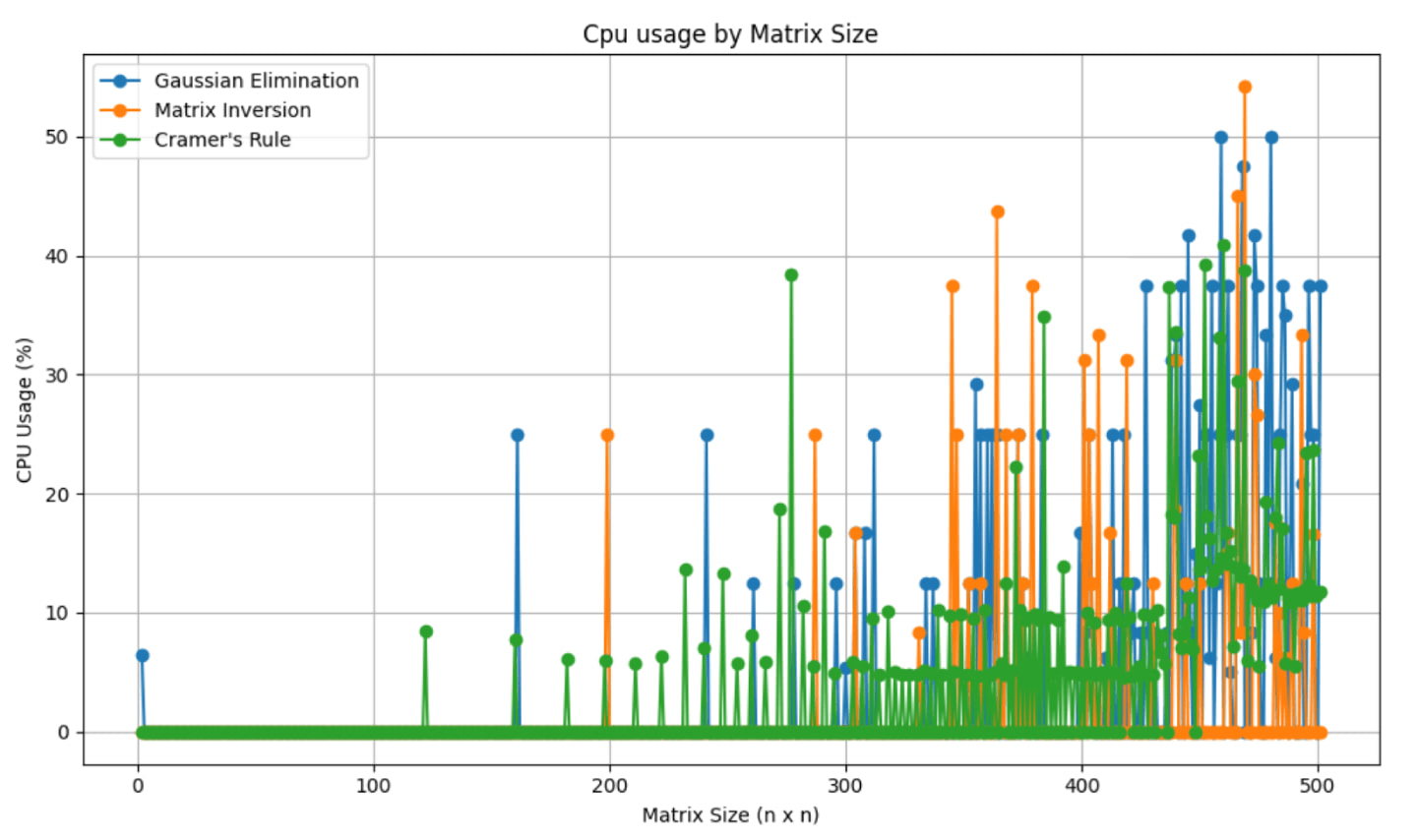
Mientras escribíamos los scripts para el proyecto, encontramos un error en una de nuestras pruebas. Cuando vimos los gráficos de los resultados del uso de la CPU, estos eran siempre constantes, independientemente del tamaño de la matriz. Sin embargo, sabíamos que esto no podía ser correcto. El coste computacional de resolver una matriz de 2 x 2 no es el mismo que el de resolver una matriz de 200 x 200.
Estuvimos tratando de resolver el problema durante cuatro horas. Probamos diferentes bibliotecas, ejecutamos el script en diferentes máquinas, añadimos más información en los archivos de registro y aislamos el método, pero nada funcionaba. Al final, uno de nosotros redujo el redondeo de los valores de uso de la CPU antes de pasarlos a la función de obtención de gráficos. Y el problema se solucionó al instante.
Cambiar tres caracteres resolvió lo que pensábamos que era un problema más grave. La experiencia nos sirvió para aprender lo importante que es comprobar meticulosamente los pequeños detalles antes de asumir que el problema necesita una solución a gran escala.
Adjuntar imágenes
Adjuntar imágenes
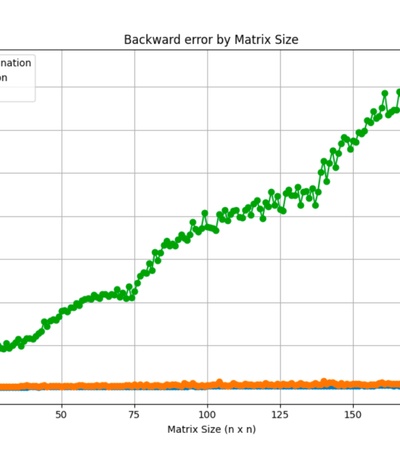
Estas imágenes son los resultados de nuestras pruebas.
Referencias
Referencias
La mayoría de los fundamentos matemáticos de nuestro proyecto se encuentran en este libro:
Stephen Friedberg, Arnold Insel, Lawrence Spence. (2018). Linear Algebra. (5.ª ed.). Pearson. ISBN 0134860241 (digital)
Descubre otros proyectos de estudiantes aquí
Descubre otros proyectos de estudiantes aquí