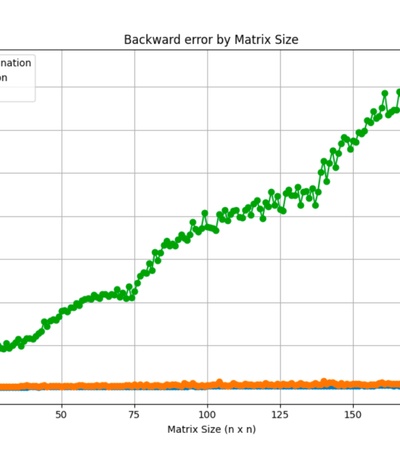
In this project, we tested and analyzed the effectiveness of various methods for solving systems of linear equations. These systems appear in many aspects of everyday life, from language models to supply chain management. Therefore, it is important to understand which methods give the most accurate and efficient results. The goal of this project was to determine which methods of solving are best suited for practical applications.
Project Overview
Project Overview
Can you provide a brief overview of the project you've been working on?
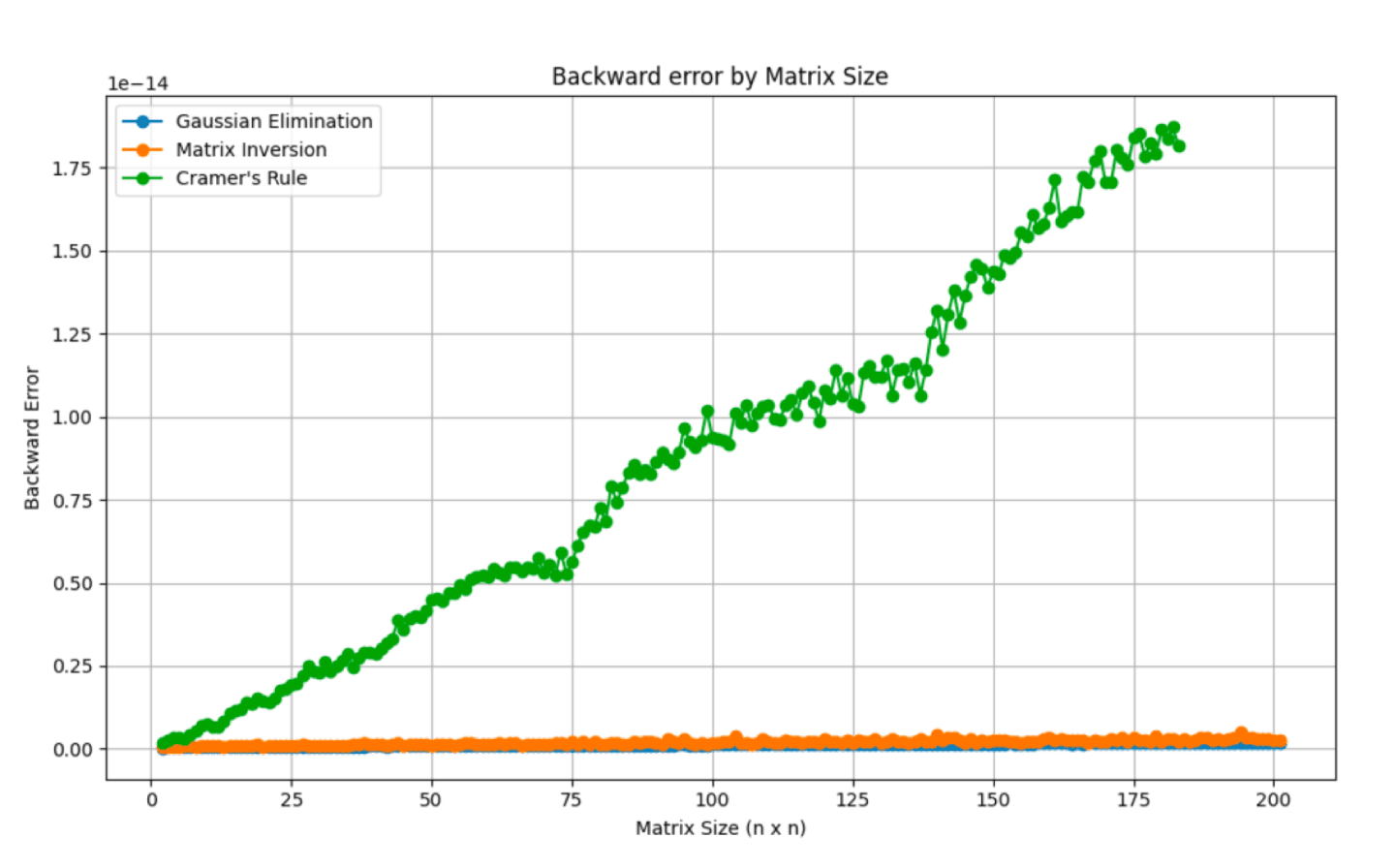
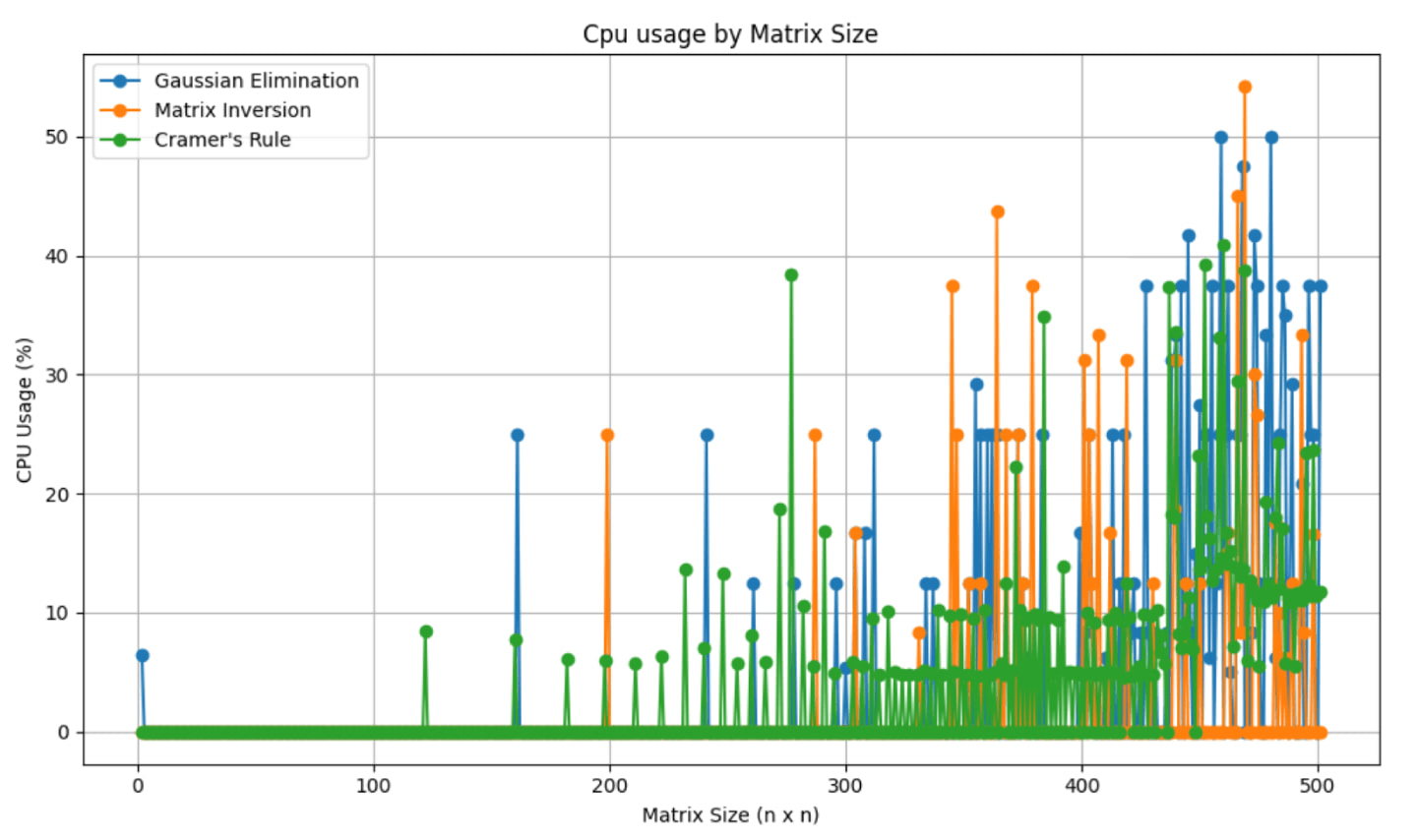
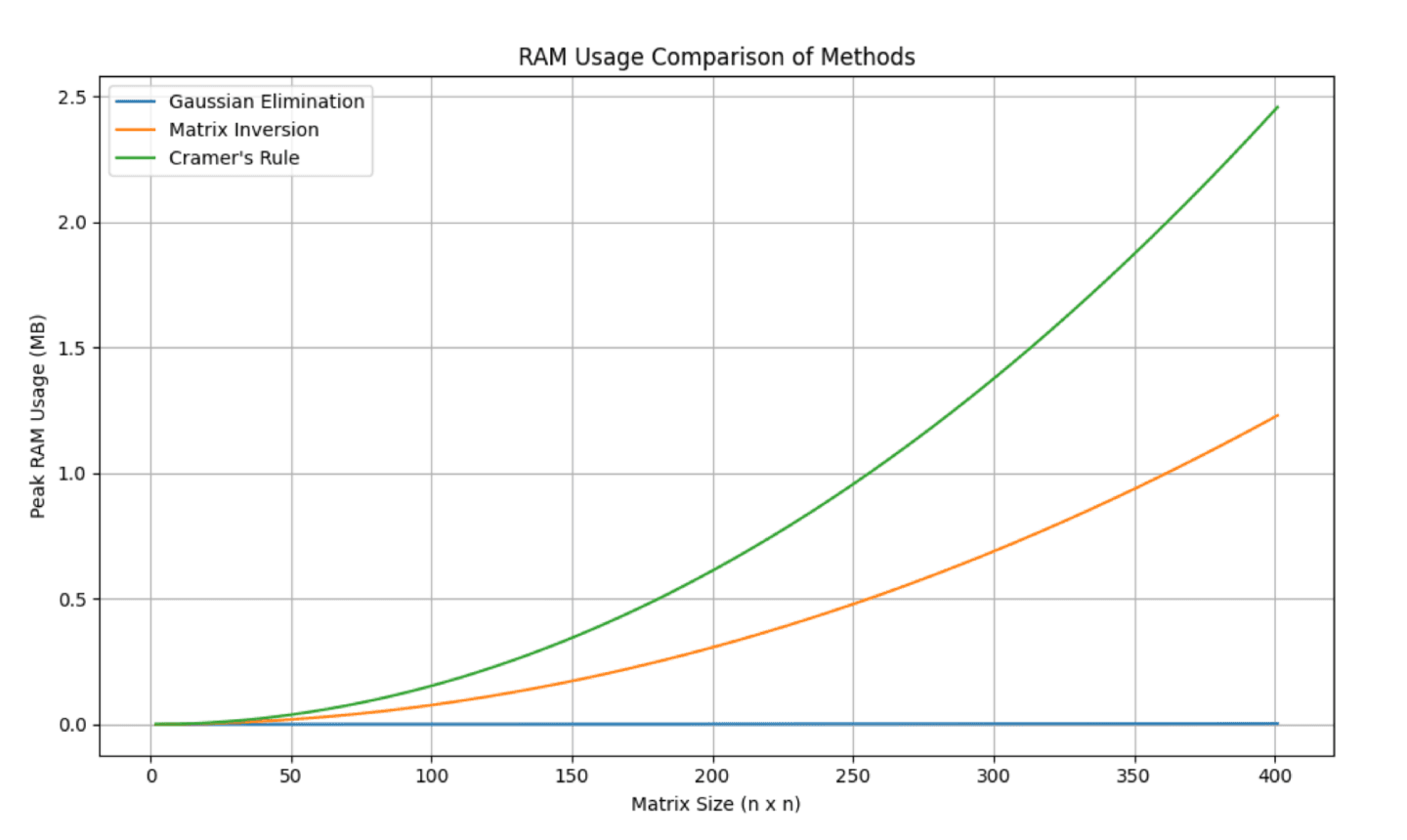
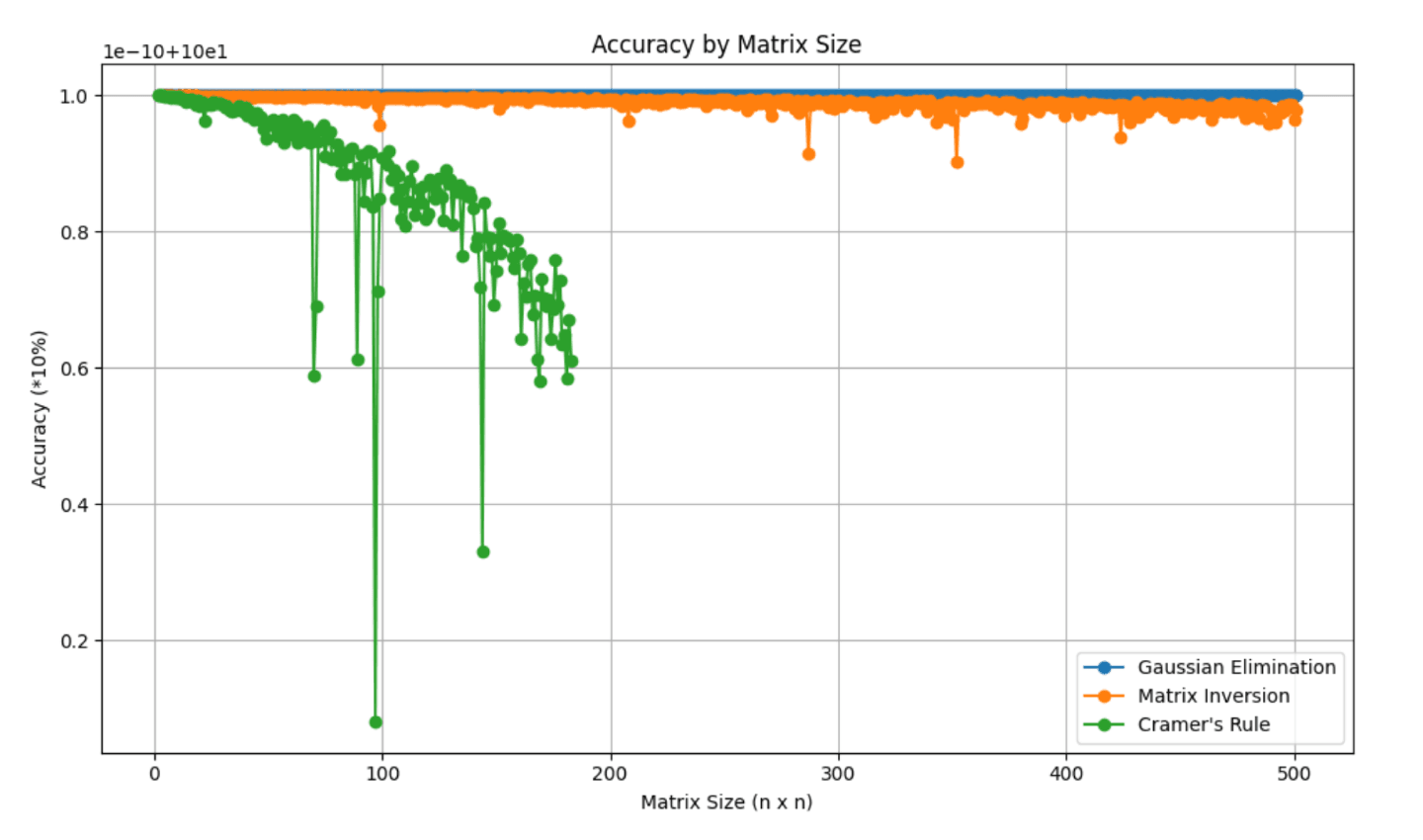
The main aim of this project is to determine the most efficient methods for solving systems of linear equations. Since most real-world applications of these systems are found in technology, our metrics for efficiency were RAM usage, CPU usage, backward error, accuracy, and computation time.To implement these tests, we generated random matrices ranging in size from 2×2 to 200×200, evaluating each method based on these performance metrics. The methods we chose to test were Cramer’s Rule, Gaussian Elimination, and Matrix Inversion, three techniques commonly used for solving linear systems. Each method was analyzed in terms of its computational complexity, numerical stability, and practicality as matrix size increased.The results were then plotted to allow us to visually analyze the method's efficiency across different matrix sizes. This visualization helped us identify how each method scales with increasing problem size, and to analyze how parameter changes affected the results.
Technical Details
Technical Details
Could you explain the technical aspects of your project? What software, tools do you use?
Our project’s objective was to compare three classical approaches for solving linear equations: Gaussian Elimination, Matrix Inversion, and Cramer’s Rule. We implemented these methods in Python, leveraging its libraries. Specifically we used NumPy for matrix operations, Matplotlib for visualization, time for execution time measurement, and psutil for monitoring RAM usage.
To systematically assess each method’s performance, we first developed a random matrix generator that created square matrices and corresponding solution vectors with customizable parameters. This allowed us to test the methods under different conditions and analyze their efficiency. For Gaussian Elimination, we leveraged NumPy’s built-in function to ensure optimal performance. Similarly, for Matrix Inversion, we used NumPy’s functions to first invert the coefficient matrix and then multiply it with the solution vector. Finally, for Cramer’s Rule, we relied on NumPy’s determinant function to repeatedly compute determinants for each variable in the system.
To evaluate the effectiveness of these methods, we conducted extensive tests focusing on accuracy, numerical stability, runtime, and resource usage. We used NumPy’s Gaussian Elimination as a benchmark to compare the accuracy of each approach. Execution time was measured using Python’s time library, while psutil was used to track computational efficiency. Our use of these tools permitted us to provide insights into the strengths and limitations of each method.
Challenges and Solutions
Challenges and Solutions
Were there any significant challenges you encountered during the project, and how did you overcome them? Can you share a specific problem-solving moment that stands out in your project?
There was a stuck-up moment where we couldn't quite successfully complete a performance test. We tried working on it simultaneously, but soon realized we were digging the hole deeper. Thus, we reorganized the tasks and rotated through them. This allowed each of us to see different parts of the project, whether it was double-checking or reformatting, and then came back individually to the problem with fresh eyes. In the end, we put together the separate brainstorm and properly and effectively implemented it.
Collaboration and Teamwork
Collaboration and Teamwork
Did you collaborate with other students or team members on this project? How did teamwork contribute to the success or progress of your project?
We were a team of four, which allowed us to split the tasks evenly and efficiently, however it was important to go back and make sure everything is linked properly. It was fundamental for the scripts to be aligned and to generate some global input parameters that would then be used along by each of us. Also, as mentioned previously, a fresh perspective can really only benefit a project. Delegating the work according to each one’s strengths and inclinations was also a beneficial factor.
Learning and Takeaways
Learning and Takeaways
What key lessons or skills have you gained from working on this project?
While writing the scripts for this project, we encountered a bug in one of our tests. When we plotted the CPU usage, it appeared constant regardless of matrix size. However, we knew this to not be correct. The computational cost of solving a 2×2 matrix was not the same as that of a 200×200 matrix.
For over four hours, the four of us attempted to resolve the issue. We tried different libraries, ran the script on different machines, added extensive logging, and isolated the method, but nothing worked. Eventually, one of us reduced the rounding of the CPU usage values before passing them to the plotting function. This instantly fixed the problem.
Changing three characters resolved what we’d assumed was a major issue. From this we collectively learned the importance of meticulously checking the small things first, rather than assuming the issue needs a large scale fix.
Attach pictures
Attach pictures
These pictures are our tests’ results.
References
References
Stephen Friedberg, Arnold Insel, Lawrence Spence. (2018). Linear Algebra. 5th. Pearson. ISBN 0134860241 (Digital)
Check other student projects
Check other student projects